概率机器人

终于拿到概率机器人这本书了，2019年第5次印刷的。

概率机器人分为4部分17章。内容比较全面，适合研究机器人的一些概念和算法。

第一部分是基础知识 第一章到第六章

第一章是绪论，主要讲述了概率机器人的这门学问，在实际的应用中用概率算法来降低不确定性的问题。

在1.2章节中 原句，不再依赖可能出现的情况的单一的“最好推测”，（读者注，这里应该是假设很差劲的最好），而是用概率算法

来表示在整个推测空间的概率分布消息。这是原话，这应该和后面的贝叶斯算法，高斯等滤波呼应。

用两个有意思的例子来阐述概率机器人：一个是有关机器人感知的；另一个是有关机器人规划和控制的。机器人定位，就是相对外部的参考系来估计机器人坐标的问题。给定环境地图，机器人需要参照传感器数据，定位自己在地图上的相对位置。已知环境中有三个相同的门，机器人的任务就是要通过检测和运动找到自己在哪。

这种定位问题被称为全局定位。在全局定位中，机器人被放置在已知的环境中的某处然后从头开始确定自己的位置。概率范式通过在整个位置空间上的一个概率密度函数来表示机器人的瞬时置信度。如图1.1a所示，所有位置具有相同的概率分布。读者注，图中的P(z|x) 本人读法为 p z given x 代表在x 发生前提下z发生的概率。他是一条黑线。

假定机器人进行了第一次传感器测量并知道自己在门附近，概率技术利用这个信息来更新置信度度，1.1b给出了后验置信度。

靠近门的位置概率较大，靠近墙处概率较小。注意分布具有三个尖峰，分别对应环境中三个完全相同的门。因此机器人并不知道自己在哪。相反，现在它有三个看起来同样合理却又不同的假设。我们发现机器人给不靠近门的位置也分配了正的概率。机器人在看到门这件事情上会犯错但这是一个非常小的非零概率。保持低概率假设对于实现鲁棒性是不可或缺的。

现在假定机器人是移动的。给出了运动对机器人置信度的影响。置信度沿运动方向移动，这反映了由机器人运动引入的不确定性。图1.1d给出了观察另一扇门后的置信度。这个观察动作使这里的算法将大概率放在了一扇门附近的位置上，机器人现在相当确信自己在哪了。最后1.1e给出了机器人继续沿着走廊运动的置信度。

这个例子阐明了概率范式。机器人感知问题用概率来描述，就是一个状态估计问题。定位实例使用贝叶斯滤波算法来进行机器人定位空间上的后验估计。信息表达方式是概率密度函数。函数的更新表示传感器测量获得了新的信息后机器人的不确定性也发生了变化。

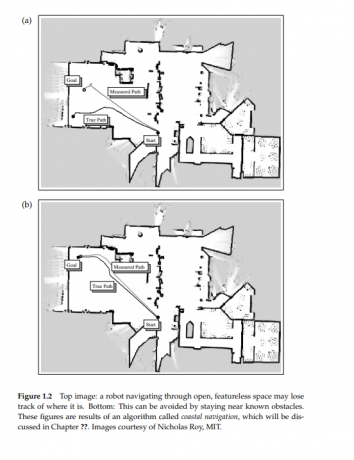
概率算法不仅能计算机器人的瞬间不确定性，也能预知未来的不确定性，并在决定正确的控制选择时，对未来不确定性进行考虑。海岸导航的例子，图中给出了一个真实建筑物的二维地图，将估计路径与真实路径进行比较，发现不是所有的轨迹所导致的不确定性水平都相同。图所示的路径引导通过相对空旷的空间，剥夺了能帮助机器人保持定位的特征。该轨迹寻找一个独特的角落，为了保持定位贴近墙壁，这并不奇怪，因为后者路径会减少不确定性，到达目标位置的机会更高些。

概率机器人将模型与传感数据进行了无缝集成，同时克服了两者的局限性；与传统的机器人编程技术相比，概率方法在面对传感器的局限和模型局限时鲁棒性更强。

概率算法最经常被提到的两个局限是计算复杂性和近似必要性，本质上比非概率算法效率低。因为它们考虑的是整个概率密度而不是单一的推测。幸运的是，不确定性有时可以用一个紧凑的参数模型（如高斯模型）很好地近似；另一方面，这样的近似在使用中太过粗略，必须使用更复杂的表达。

目前先这么多。