轨迹处理系列：轨迹图形的平移变换算法

机器人会在户外形成一条作业轨迹，该轨迹是根据北斗定位传感器采集的经纬度点，该轨迹是经纬度的集合。 G = [LONGITUDE i,LATITUDE i],i∈（0，n）

现在我们需要对该轨迹的集合进行图形化处理。

由于该轨迹是圆形地球的经纬度坐标，如果要转换到笛卡尔直角坐标系中需要经过一个高斯变换，也就是认为格林尼治 赤道那里认为是迪卡尔坐标系的

原点（0，0）.

平面直角坐标系高斯变换要将经纬度转换成平面的x,y坐标。可以通过换算每个纬度的分辨率是几公里，经过换算得到距离坐标。

具体实现方式可见 

https://blog.csdn.net/niu_88/article/details/97690318

知道了南北向的子午圈曲率半径，东西向的平行圈曲率半径，地球表面的经纬度为lat、lon（弧度），则转为平面坐标为：

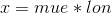
在我们的实际应用中我们将上述得到的 x,y 坐标值需要经过平移和缩放算法被包含于我们1024x1024像素的图片中去。

那么我们的1024x1024的图片的左下角就可以认为是 起始原点（0，0），而经纬度坐标转换出来的值片段

 x,y
12778764.000,2988459.000
12778765.000,2988459.000
12778766.000,2988461.000
12778767.000,2988463.000
12778769.000,2988464.000
12778771.000,2988465.000
12778772.000,2988466.000
12778774.000,2988466.000

最终需要将上述的x和y坐标放到我们有限的直角坐标中去xlimit =1200,y limit =1200.

最终确定在轨迹不失真的情况下，需要确定步骤如下：

  1 确定是否需要缩放和缩放比例

  2 确定x轴和y轴平移数据

  3 转换坐标到尺寸内

先缩放到尺寸内，再平移。

 1 确定是否需要缩放和缩放比例

 a 查找x坐标值xmax最大值和最小值xmin,求差找到Δx

 b 查找y坐标值最大ymax值和最小值ymin找到Δy

 c 比较Δx和Δy 的大小，以最大值和1024进行比较确定放大缩放比例值。

d 缩放大比例值为float k_theta=   Δx>Δy ? (float)Δx/1024 : (float)Δy/1024

  2 确定x轴和y轴平移数据

a 确定x轴的中心点，xcenter =xMin+Δx/2 

b 确定y轴的中心点  ycenter =yMin+Δy/2

c 最终中心为 （1024/2,1024/2）

d 确定平移距离 movex =xMin+Δx/2  

  3 转换坐标到尺寸内

下中，xi,yi为第i个坐标值。

 long unsigned  int gx =  int(xi- movex)/(k_theta) + Map_Size/2;
long unsigned  int gy = Map_Size - (int(yi- movey)/(k_theta) + Map_Size/2);

这里先将第i个坐标值进行缩放大后，同时平移的距离也要缩放大。在缩放大完成后符合1024的坐标后再进行坐标中心的平移，否则会溢出。

可以认为1024尺寸是在完成缩放大后使单位相同后进行加减的。

opencv的坐标在左上角，需要1024 - 值。